We call “pesanteur” (heaviness; gravity) the force by which every body being left to itself falls toward the surface (center) of the earth. The same force makes bodies fall when there is no obstacle to intervene to impede their fall (InstPhy, § 294). Du Châtelet adds that  produces either a dead force or a living force, according to the circumstances in which it acts. This means

When nothing resists bodies, a living force arises in these Bodies, since it makes them fall toward the surface of the earth. When Bodies are resisted by an invincible obstacle, the force reamins dead; for it does not produce any effect (InstPhy, § 296).

For today’s readers the correlation between heaviness and dead/living forces is is not easy to understand. One has to bear in mind Galileo’s principle that a body falling through a given height acquires a velocity just great enough to raise it to the same height. Why? The law of (parabolic) fall claims that the distance traveled by a falling body is directly proportional to the square of the time it takes to fall. For example: A stone falling for twice as long as another stone will travel four times the distance.

In his Discours de métaphysique (1686, § 17) Leibniz claimed that a body that falls from a certain height acquires the same force that is necessary to elevate it to that height (excluding external interference, such as friction). Now, Galileo had shown experimentally that the velocity a body acquires in free fall is proportional to the square of the distance fallen. According to Leibniz’s argument, therefore, it is not the (Cartesian) quantity of motion (mass times velocity) that is conserved, but the motive force. This quantity is represented as the product of the mass and the square of velocity.

From today’s perspective this hypothesis entails the later expression for gravitational potential energy which is equal to the work done against gravity to bring a mass to a given point in space. If an object falls, it gives up its gravitational potential energy. The gravitational force does work on it, and speeds it up. Its gravitational potential energy is converted into kinetic energy.

According to Du Châtelet, we owe Galileo Galilei two important insights: Firstly, Galileo realized that (in a vacuum) all bodies fall at the same rate relative to the earth. This contradicted Aristotle’s long-accepted idea that heavier objects fell faster. Two bodies released from a given height will reach the ground (in general) at different times because they are affected by air friction differently (InstPhy, § 300):

donc, conclut Galilée, la résistance des milieux, & la grandeur, & l’aspérité de la surface des différens corps, sont les seules causes qui rendent la chûte des uns plus prompte que celle des autres. (Amsterdam 1742)

therefore, Galileo concluded, the resistance of the media, and the size and roughness of the surface of different Bodies, are the only causes that make the fall of some faster than that of others. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

In the same paragraph Du Châtelet quotes from Galileo’s First Dialogue in Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla mecanica & i movimenti locali (Opere di Galileo Galilei nobile Fiorentino primario filosofo, e mattematico del serenissimo granduca di Toscana, vol. 2. Firenze: G. Tartini 1718, 55):

Che se si levasse totalmente la resistenza del mezzo, tutte le materie descenderebbero con eguali velocita.

That if one completely removed the resistance of the medium, all matter would descend with equal velocity. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

Lucretius has already expressed Galileo’s decisive insight that objects of any weight fall toward the Earth at the same rate (InstPhy, § 301):

Lucrèce lui-même, tout mauvais physicien qu’il étoit d’ailleurs, avoit entrevû cette vérité, & l’a exprimée dans son deuxieme livre par ces deux vers.

Lucretius himself, however bad a Physicist he was otherwise, glimpsed this truth, and expressed it in the second Book by these two lines. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

Du Châtelet quotes from Lucretius’ very popular De rerum natura, a poem which consists of six books, in dactylic hexameters (Book II, 238-9):

Omnia qua propter debent per inane quietum

Aeque ponderibus non aequis concita ferri.

wherefore all things must needs be borne on through the calm void,

moving at equal rate with unequal weights. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

Galileo’s second important discovery was that bodies fall on the surface of the earth at a constant acceleration. Here is, says Du Châtelet, how Galileo expressed himself this fact in the First Dialogue (Dialogo Primo, 56):

Dico per tanto che un corpo grave ha de natura intrinseco principio di muoversi verso ’l comun centro de i gravi eioe del nostro globo terrestre, con movimento continuamente accelerato.

I say that a heavy body has from nature an intrinsic principle of moving towards the common centre of heavy objects; that is to say, to the centre of our terrestrial globe, with a continually accelerated motion. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

Du Châtelet emphasizes that Galileo’s law of free fall is experimentally and geometrically well confirmed, so that nobody could doubt its correctness. In its original formulation, the law of free fall states that bodies in falling toward the earth traverse spaces that are as the squares of the times of their fall, or as the squares of the speeds acquired in falling (InstPhy, § 313). Du Châtelet refers to experiments of Giovanni Battista Riccioli and Francesco Maria Grimaldi in order to underscore this hypothesis (InstPhy, § 311):

Riccioli & Grimaldo, cherchèrent, comme avoit fait Galilée, à s’assurer de cette vérité par la experience. Ils firent tomber des mobiles du haut de plusieurs tours différemment élevées, & ils mesurèrent le tems de la chute des Corps qui tomboient de ces différentes hauteurs par les vibrations d’un pendule, de la justesse duquel Grimaldo s’étoit assuré en comptant le nombre de ses vibrations, depuis un passage de l’étoile de la queue du lion par le Méridien jusqu’à l’autre. Ces deux savans Jésuites trouverent par le résultat de leurs expériences, que ces hauteurs étoient exactement comme les quarrés des tems des chûtes. (Amsterdam 1742)

Riccioli and Grimaldo, sought, as had Galileo, to ascertain this truth by experiment. They made moveable bodies fall from the top of several towers of different heights, and they measured the time of the fall of these bodies from these different heights by the vibrations of a pendulum, the accuracy of which Grimaldo ascertained by counting the number of its vibrations from one passage of the tail of the Lion through the Meridian until the next. These two Jesuit scholars found from the result of their experiments that these different heights were exactly as the squares of the times of the falls. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

The Italian astronomer Giovanni Battista Riccioli is commonly credited with performing the first precise experiments to determine the acceleration of a freely falling body, confirming that the distance of fall was proportional to the square of the time taken. Riccioli was an Italian Jesuit working in Bologna with Francesco Maria Grimaldi. Furthermore, Grimaldi and Riccioli indirectly measured gravity very accurately using a pendulum by recording the oscillations of a pendulum. The time it takes a pendulum to complete one back-and-forth swing, called the pendulum’s period, depends only on the pendulum’s length and the value of gravity (InstPhy, § 311).

An apparatus that makes use of another important physical principle discovered by Galileo – the isochronism of pendulums of equal length – was invented in 1699 by Jean Truchet (known as Father Sébastien) to demonstrate Galileo’s law of falling bodies along an inclined plane. It provides an experimental demonstration of the acceleration of natural motion using an equivalent but different approach with respect to the inclined plane (InstPhy, § 314).

Le Père Sébastien, ce Géometre des sens, avoit imaginé une Machine composée de quatre paraboles égales, qui se coupoient à leur sommet; & au moyen de cette Machine dont on trouve la description & la figure dans les Mémoires de l’Académie des Sciences, A. 1699, il démontroit aux yeux du corps, du témoignage desquels les yeux de l’esprit ont presque toujours besoin, que la chûte des corps vers la terre s’opere selon la progression découverte par Galilée. (Amsterdam 1742)

Father Sebastien, that Geometrician of the senses, devised a Machine made of four equal parabolas that intersected at their tips; and by means of this Machine, of which we find the description and diagram in the Mémoires de l’Académie des Sciences A. 1699, he demonstrated to the corporeal eye, the witness of which the mind’s eye almost always needs, that the fall of bodies toward the earth operates according to the progression discovered by Galileo. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

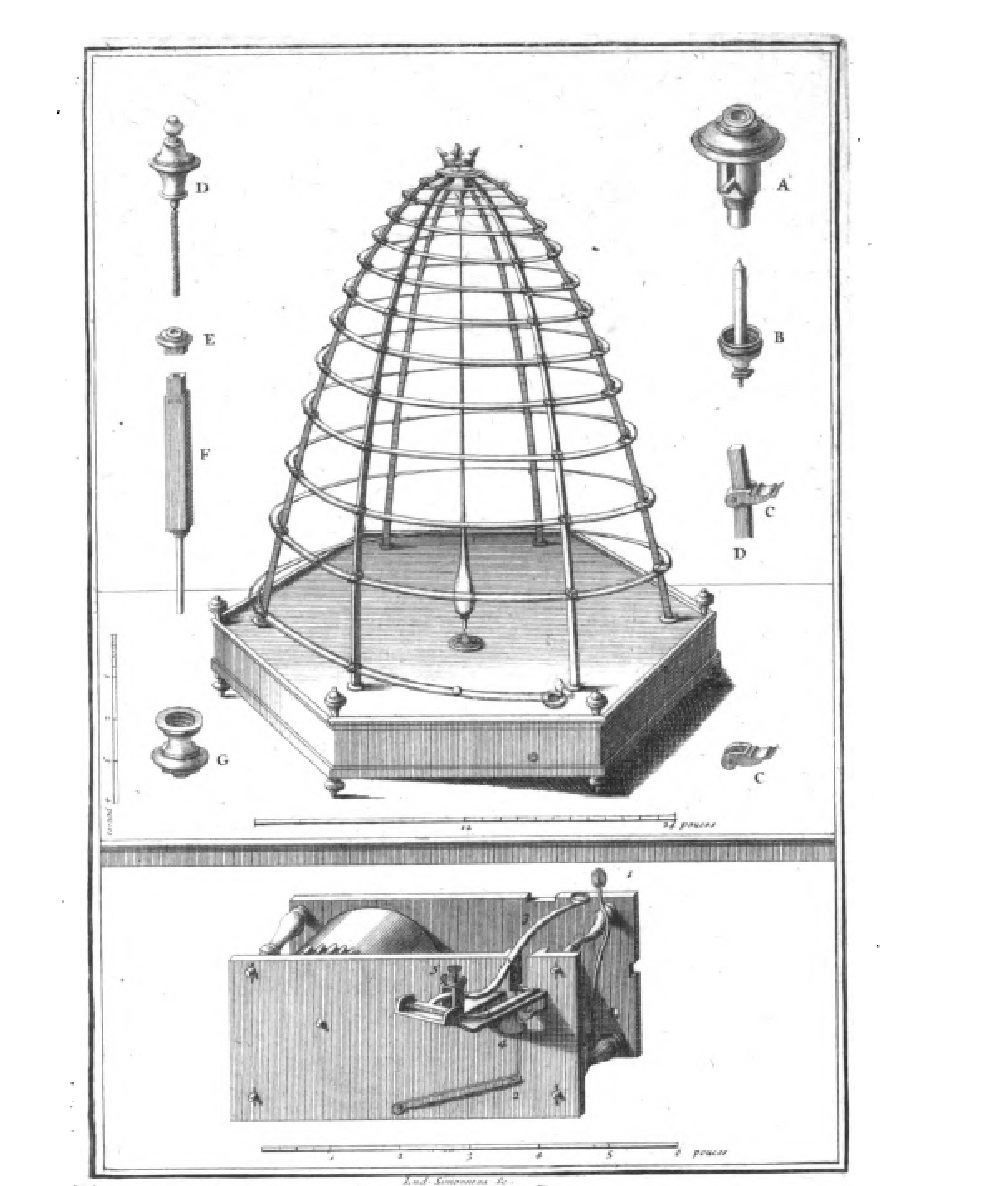
Father Sebastien gave an exact description of the apparatus in the Mémoires de l’Académie des Sciences 1699 («Explication de la machine qui a été faite pour examiner l’accélération des boules qui roulent sur um plan incliné, et la comparer à celle de la chute des corps», ann. 1699, p. 283). The illustration of the apparatus shown here can also be found in this article. The apparatus consists of a hexagonal wooden base. A pair of metal wires is wound in a spiral around the paraboloid, forming a track that rises from the base to the top of the device. At the apex of the paraboloid is a cup with a hole connecting it to the spiral track. A ball is dropped down the track. When the ball has completed the first turn of the spiral, the second ball is released. In accordance with Galileo’s law one can observe that each turn, whose length increases in the sequence of odd numbers beginning with 1, is covered by both balls in equal times.

Galileo himself used an inclined plane to accurately measure free fall. The experiment consists in releasing a small ball from the top end of the plane at the same time as the pendulum is swung. At each successive complete oscillation of the pendulum, the ball strikes one of the small bells placed along the inclined plane at increasing distances, arranged in the sequence of odd numbers. Du Châtelet summarizes Galileo’s own description of the inclined plane in the “Third Day” in Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla mecanica & i movimenti locali (Opere di Galileo Galilei nobile Fiorentino primario filosofo, e mattematico del serenissimo granduca di Toscana, vol. 2. Firenze: G. Tartini 1718 [first published 1638]) as follows (InstPhy, § 310):

Galilée ayant démontre ce qui arriveroit à un mobile qui tomberoit vers la terre par un mouvement étalement accéléré, chercha a s’assurer par l’expérience que la nature suit réellement cette proportion, dans la chute des graves. Il imagina, pour y parve- terre fenir, une expérience très-ingénieuse. Il fit un grand tuyau de bois haut de douze coudées, & large environ d’un pouce, au dedans duquel il colla un parchemin très-léger, afin qu’il fût uni autant qu’il le pouvoit être; & ayant élevé le bout supérieur de ce tuyau sur un plan horisontal de la hauteur d’une, de deux, & successivement de plusieurs coudées, ce qui en faisoit un’ plan incliné, il laissa tomber successivement de la longueur entière, ou du quart, ou de la moitié de ce tuyau, une petite boule de cuivre parfaitement ronde, & parfaitement polie, & il trouva toujours dans les expériences, qu’il assure avoir répétées jusqu’à cent fois, que les tems de la chute étoient en raison soudoublée des espaces parcourus; or, en faisant un plan incliné de ce tuyau dans lequel la boule tomboit, Galilée rallentissoit le mouvement du mobile, & en rendoit, par ce moyen, la vitesse discernable, ce qui n’eût pas été possible dans une chute perpendicuaire aussi courte; car les corps tombent plus lentement par un plan incliné, que par une ligne perpendiculaire, & ils suivent les mêmes loix dans l’une & le autre de ce chutes, comme vous le verrez aux §. 425 & § 428; ainsi, il lui étoit aisé de sçavoir par ce moyen quel espace la pésanteur faisoit parcourir au mobile pendant un certain tems, & il mesura ce tems par la quantité d’eau qui s’étoit écoulée d’un vase pendant que le corps parcouroit ces différens espaces. (Amsterdam 1742)

Galileo, having demonstrated what must happen to a moveable body that would fall toward the earth in an equally accelerated motion, sought to ascertain through experimentation that nature really follows this proportion in the fall of weights. To achieve this, he devised a very ingenious experiment. He made a large wooden tube twelve cubits long and about an inch wide; to the inside of which he glued a very light parchment, so that it was as smooth as it could be; and having raised the upper end of this channel on a horizontal plane to the height of one, two, and successively of several cubits, in such a way that this channel became an inclined plane, he let a small copper ball, perfectly round and perfectly polished, fall along the channel, and in making it fall successively the entire length of this channel, or a quarter of it, or a half, he always found in his experiments, that he asserts he had repeated up to a hundred times, that the times of the fall were as the square root of the spaces traversed. Now, in making an inclined plane of this channel along which the ball was falling, Galileo slowed the motion of the moveable body, and by this means made the speed discernible, which would not have been possible in a perpendicular fall that short; for bodies fall more slowly along an inclined plane than along a perpendicular plane, and they follow the same laws in both of these falls (§ 425 & § 428). Thus it was easy for him to know by this means what space heaviness made a moveable body traverse during a certain time, and he measured this time by the quantity of water that flowed from a vessel while the body traversed these different spaces. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

Du Châtelet had carefully studied Galileo’s experiment of the inclined plane. Her description of a wooden tube twelve cubits long and about an inch wide (InstPhy, § 310) is exactly the same one can find in Galileo’s Dialog. In order to measure the velocity of a falling object one has to measure distances and times. The path of a falling object can be analyzed using a graph in terms of change along the y axis and change along the x axis. The ratio of those quantities, called the slope, tells about the rate of change of the curve at the point in question. That seems trivial today, but it wasn’t at Du Chatelet’s time.

The crucial question which led to the discovery of the infinitesimal calculus was: What happens when segments under investigation are broken down into smaller and smaller parts? Given that time is composed of an infinite number of instants (just like a geometrical line is composed of an infinite number of points), and that the total speed of fall is composed of an infinite number of degrees of speed (just as a triangle is composed of an infinite number of lines) one yielded the law that distance is proportional to time squared.

Du Chatelet sums up the results as follows (InstPhy, § 315):

1. Que la force qui fait tomber les corps est toujours uniforme, & qu’elle agit également sur eux à chaque instant.

2. Que les corps tombent vers la terre d’un mouvement uniformément accéléré.

3. Que leurs vîtesses sont comme les tems de leur mouvement.

4. Que les espaces qu’ils parcourent sont comme les quarrés des tems, ou comme les quarrés des vîtesses ; & que par conséquent les vîtesses & les tems sont en raison sous-doublée des espaces.

5. Que l’espace que le corps parcourt en tombant pendant un tems quelconque, est la moitié de celui qu’il parcourroit pendant le même tems d’un mouvement uniforme avec la vîtesse acquise; & que par conséquent cet espace est égal à celui que le corps parcourroit d’un mouvement uniforme avec la moitié de ces vîtesses.

6. Que la force qui fait tomber ces corps vers la terre, est la seule cause de leur poids, car puisqu’elle agit à chaque instant, elle doit agir sur les corps, soit qu’ils soient en repos, soit qu’ils soient en mouvement; & c’est par les efforts que ces corps font sans cesse pour obéir à cette force, qu’ils pesent sur les obstacles qui les retiennent. (Amsterdam 1742)

1. That the force that makes bodies fall is always uniform, and that it acts equally upon them at each instant.

2. That bodies fall toward the earth in a uniformly accelerated motion.

3. That their speeds are as the time of their motion.

4. That the spaces that they traverse are as the squares of the times or as the squares of the speeds; and that consequently the speeds and the times are as the square roots of the spaces.

5. That the space that the body traverses in falling during a given time is the square root of that which it would traverse during the same time with a uniform motion that is the sum of the acquired speeds; and that consequently this space is equal to that which the body would traverse with a uniform motion that is half of these speeds, etc.

6. That the force that makes bodies fall toward the earth is the sole cause of their weight; for since it acts at each instant, it must act on the bodies whether they are at rest or in motion; and it is through the unceasing efforts that bodies make to obey this force that they weigh upon the obstacles that restrain them. (Copyright © 2018 KB)

[ Manuscript Bibliotheque nationale de France (Paris), Fonds français 12265 ]

Thus, the heights to which bodies can reascend by the speed acquired in falling are always as the square of their speeds: «Ainsi, les hauteurs auxquelles les corps peuventre monter par la vitesse aquise en tombant, sont toujours comme le quarré de leurs vitesses» (InstPhy, § 320).

******************

Under the entry PESANTEUR, s. f. (Phys.) in d’Alembert’s and Diderot’s Encyclopédie large passages are taken verbatim from Du Châtelet’s Chapter 13. See also the entry “Pesanteur” in: Johann Heinrich Samuel Formey (ed.): Dictionnaire instructif, où l’on trouve les principaux termes des sciences et des arts dont l’explication peut être utile ou agréable aux personnes qui n’ont pas fait des études approfondies. Halle: Gebauer 1767.

Back to main project | Next chapter